Cara Menghitung Rumus Luas Segitiga Lengkap dengan Contoh Soal
Apakah kalian tahu apa
itu segitiga? Segitiga adalah sebuah bangun datar yang memiliki tiga buah sisi
dimana setiap sisi tersebut bertemu pada tiga buah titik sudut. Ini dia gambar
dari segitiga:
Menurut euclid, jumlah keseluruhan sudut yang ada pada segitiga adalah
1800. Oleh karenanya kita bisa menghitung sakah satu sudut segitiga
apabila sudut-sudut yang lain bisa diketahui. Postingan ini akan membahas
secara lengkap mengenai rumus luas segitiga serta contoh soal mengenai segitiga
dan cara menjawabnya.
Rumus mencari luas segitiga
lengkap
Sebelum kita mempelajari rumus mencari luas segitiga mari kita cari
tahu terlebih dahulu jenis-jenis segitiga yang ada.
Jenis-jenis segitiga
Dengan berdasarkan kepada panjang sisi yang ada pada suatu segitiga,
maka jenis segitiga dapat dibagi menjadi 3, yaitu:
Segitiga sama sisi
Merupakan segitiga yang panjang setiap sisinya sama dan masing-masing
sudut yang ada pada segitiga sudut tersebut sama besar yaitu 600
Segitiga sama kaki
Merupakan segitiga yang memiliki dua sisi yang sama panjang sementara
satu sisi yang lain berbeda. Oleh karenanya, dua buah sudut yang ada sama
besarnya.
Segitiga sembarang
Merupakan segitiga yang panjang masing-masing sisinya berbeda-beda.
Tiap sudut pada segitiga sembarang juga berbeda besarnya.
Bila dibedakan berdasarkan besar sudut yang ada pada segitiga, maka
segitiga dapat dibedakan menjadi:
Segitiga siku-siku
Adalah segitiga dimana salah satu sudutnya memiliki besar 900.
Sisi yang berada tepat didepan sudut siku-siku tersebut dinamakan sebagai
hipotenusa.
Segtiga lancip
Adalah segitiga yang besar dari ketiga sudutnya kurang dari 900
Segitiga tumpul
Adalah segitiga dimana salah satu sudutnya memiliki besar sudut lebih
dari 900.
Rumus untuk menghitung luas
segitiga
Luas dari sebuah segitiga dapat dicari dengan menggunakan rumus
L = ½.alas.tinggi
Sementara rumus keliling segitiga adalah:
K = sisi1 + sisi2 + sisi3
Teorema Heron
teorema ini biasa digunakan untuk mengetahui luas dari segitiga
sembarang. misalkan sisi-sisi pada segitiga tersebut dilambangkan dengan
huruf a, b, dan c maka rumus luasnya adalah:
dimana
Sedangkan pada segitiga sama sisi dimana sisinya adalah a maka luas dan kelilingnya bisa diketahui melalui rumus berikut ini:
Contoh Soal untuk Rumus Luas Segitiga
Contoh Soal 1
Diketahui luas dari sebuah segitiga yang panjang alasnya 24 cm adalah 180
cm2. Hitunglah tinggi dari segitiga tersebut.
Jawab:
Luas Segitiga = ½ x alas x tinggi
180 cm2= ½ x 24 cm x
tinggi
180 cm2= 12 cm x tinggi
tinggi = 180 cm2/12 cm
tinggi = 15 cm
Contoh Soal 2
Hitunglah Luas dari sebuah segitiga yang memiliki panjang
alas 6 cm dan tinggi 8 cm
Jawab:
L = ½ x alas x tinggi
L = ½ x 6 cm x 8 cm
L = 24 cm2
 adalah semiperimeter
adalah semiperimeter 
 ,
, 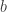
 dengan
dengan  sebagai alasnya dan
sebagai alasnya dan 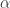 sudut diantara
sudut diantara  dan
dan 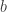 . Untuk membuktikan rumus heron, kita menggunakan hukum cosinus
. Untuk membuktikan rumus heron, kita menggunakan hukum cosinus





